알고리즘 복잡도가 필요한 이유
한 가지 결과를 도출해내기 위해서도 여러 가지 알고리즘이 존재하게 된다. 그중에서도 가장 빠르고 효율적인 알고리즘을 분석하기 위해서 복잡도가 필요하다. 즉, 가장 빠르게 실행되는 알고리즘을 찾는 방법이라고 볼 수 있다.
복잡도 계산 항목
복잡도 계산 항목에는 2가지 항목이 있다. 한 가지는 시간 복잡도이며 나머지 한 가지는 공간 복잡도이다.
| 시간 복잡도 | 알고리즘의 실행 속도 |
| 공간 복잡도 | 알고리즘이 사용하는 메모리 사이즈 |
최근 대부분의 메모리는 많이 발전되어 알고리즘 작성 시메모리 부분은 크게 신경을 쓰지 않아 주로 시간 복잡도를 기준으로 알고리즘을 분석한다.
알고리즘 성능 표기법
알고리즘 성능 표기법에는 3가지 표기법이 존재한다.
| Big-O 표기법 | 알고리즘의 최악의 실행 시간을 표기한다. |
| Ω(오메가)표기법 | 알고리즘의 최상의 실행 시간을 표기한다 |
| θ(세타)표기법 | 알고리즘의 평균 실행 시간을 표기한다 |
가장 일반적이고 많이 사용되는 표기법은 Big-O표기법이다. 아무리 최악의 상황이라도 최소 이 정도의 성능은 보장한다는 의미이기 때문이다.
Big-O 표기법
O(n)으로 표기한다. O(n)은 입력값 n에 따라 결정되는 시간 복잡도 함수이다. O(1), O(logn), O(n), O(nlogn), O(n2), O(2n), O(n!) 등으로 표기한다.
시간 복잡도 크기 순서는 O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(2n) < O(n!) 이다. 아래의 그림과 같이 입력되는 n의 크기에 따라 시간 복잡도가 기하급수적으로 늘어날 수 있다.
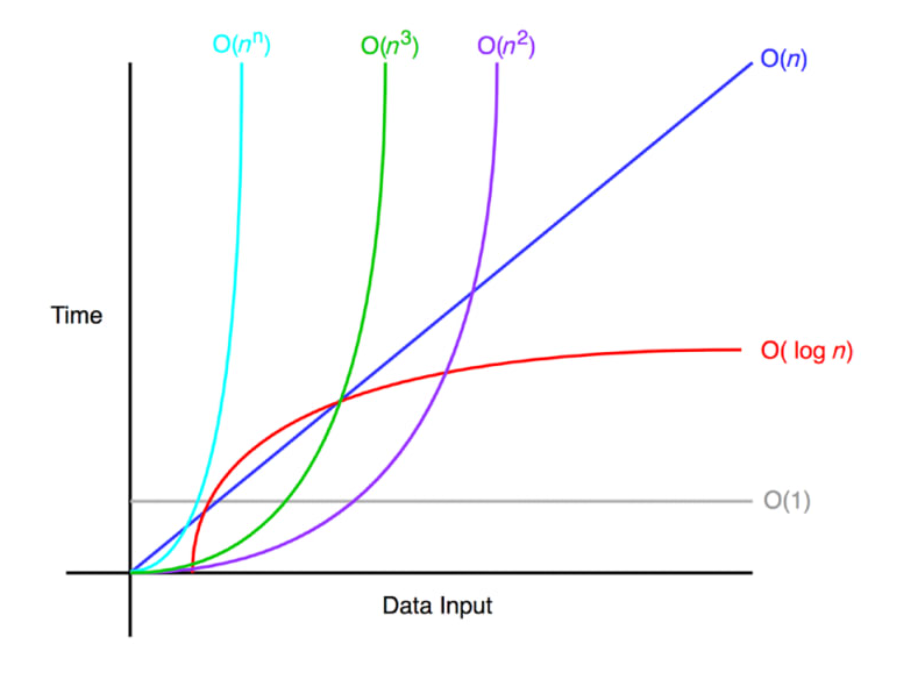
아래의 if문의 실행 횟수는 n이 1이든 10이든 100이든 무조건 한 번이다. 따라서 Big-O표기법으로 표현 시 O(1)이라고 할 수 있다.
if ( n<10 ){ ... }
아래의 for문의 실행 횟수는 n의 입력값이 1이면 1회 2이면 2회인 것과 같이 입력된 n의 값만큼 반복문이 반복하게 된다. 따라서 Big-O표기법으로 표현 시 O(n)이라고 할 수 있다.
for (int i = 0 : i < n ; i++) { ... }
아래의 for문의 실행 횟수는 n의 입력값이 1이면 1회 2이면 4회 3이면 9회인 것과 같이 입력된 n의 제곱 값만큼 반복문이 반복하게 된다. 따라서 Big-O표기법으로 표현 시 O(n2)이라고 할 수 있다.
for(int i = 0 : i < n ; i++){
for(int i = 0 : i < n ; i++){
...
}
}
간단한 예제들로 Big-O의 표기법을 예로 들어봤지만 확실한 한 가지는 알고리즘의 대부분을 차지하는 변수 대입, 조건문, 반복문 중에 반복문이 알고리즘의 효율성 즉 시간 복잡도에 가장 많은 영향을 끼친다는 것이다. 마지막 아래의 예제를 보면 반복문의 중요성을 더 확실하게 알 수 있다.
//1부터 n까지의 합을 구하는 알고리즘
//1번
public int sum(int n) {
int total = 0;
for (int i = 1; i <= n; i++) {
total += i;
}
return total;
}
//2번
public int sum(int n) {
return n * (n + 1) / 2;
}
1부터 n까지 합을 구하는 방법이다. 1번 알고리즘은 입력 n에 따라 덧셈을 n번 진행해야 하기 때문에 O(n)이라고 할 수 있다. 하지만 2번 알고리즘은 1번과 완전히 같은 결과를 도출해 내지만 입력 n이 어떤 숫자이든 한 번만 실행되기 때문에 O(1)이라고 할 수 있다. 이와 같이 반복문이 알고리즘의 효율성에 큰 영향을 미친다는 것을 알 수 있다.
'자료구조' 카테고리의 다른 글
| Hash Table (0) | 2021.10.24 |
|---|---|
| Double Linked List (0) | 2021.10.15 |
| Single Linked List (0) | 2021.10.15 |
| Stack (0) | 2021.10.15 |
| Queue (0) | 2021.10.15 |
